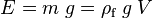ARQUIMEDES

 Arquimedes fue un matemático griego, estudió en Alejandría, donde tuvo como maestro a Conón de Samos y entró en contacto con Eratóstenes; a este último dedicó Arquímedes su Método, en el que expuso su genial aplicación de la mecánica a la geometría, en la que pesaba imaginariamente áreas y volúmenes desconocidos para determinar su valor. Regresó luego a Siracusa, donde se dedicó de lleno al trabajo científico.

La idea de Arquímedes está reflejada en una de las proposiciones iniciales de su obra Sobre los cuerpos flotantes, pionera de la hidrostática; corresponde al famoso principio que lleva su nombre y, como allí se explica, haciendo uso de él es posible calcular la ley de una aleación, lo cual le permitió descubrir que el orfebre había cometido fraude.

COMO DESCUBRIO QUE LA CORONA DEL REY NO ES AUTENTICA

Sabiendo el volumen y el peso, Arquímedes podría determinar la densidad del material que componía la corona. Si esta densidad era menor que la del oro, se habrían añadido materiales de peor calidad (menos densos que el oro), por lo que el orfebre habría intentado engañar al rey.

Así tomó una pieza de plata del mismo peso que la corona, y otra de oro del mismo peso que la corona. Llenó una vasija de agua hasta el tope, introdujo la pieza de plata y midió la cantidad de agua derramada. Después hizo lo mismo con la pieza de oro. De este modo, determinó qué volumen equivalía a la plata y qué volumen equivalía el oro.

Repitió la misma operación, pero esta vez con la corona hecha por el orfebre. El volumen de agua que desplazó la corona se situó entre medias del volumen de la plata y del oro. Ajustó los cálculos y determinó de forma exacta la cantidad de plata y oro que tenía la corona, demostrando así ante el rey Hierón II que el orfebre le había intentado engañar.

PRINCIPIO DE ARQUIMEDES

El principio de arquimedes  es un principio físico que afirma que: «Un cuerpo total o parcialmente sumergido en un fluido en reposo, recibe un empuje de abajo hacia arriba igual al peso del volumen del fluido que desaloja». Esta fuerza¹ recibe el nombre de empuje hidrostatico  o de Arquímedes, y se mide en newtons (en el SI). 

COMO ESTABLCE QUE UN OBJETO SE HUNDE O FLOTA EN UN FLUIDO

Arquímedes observó que al introducirse en el agua, el nivel de ésta subía. Consideró que la cantidad de agua desplazada estaba en relación con su peso. Pensó entonces que con la corona ocurría lo mismo y como el peso (en realidad la masa) dependía de su densidad, una corona que no fuera sólo de oro, desplazaría una cantidad de agua diferente a una de oro puro. Esta experiencia dio pauta para que Arquímedes resolviera el problema de la corona, pero además le permitió establecer lo que ahora conocemos como principio de Arquímedes

FORMULA QUE PROPONE ARQUIMEDES

la formula que propone arquimedes son las siguientes:

                                               

                                                                     o bien

                                               

donde E es el empuje, ρ_f es la densidad del fluido, V el «volumen de fluido desplazado» por algún cuerpo sumergido parcial o totalmente en el mismo, g la aceleración de la gravedad y m la masa. De este modo, el empuje depende de la densidad del fluido, del volumen del cuerpo y de la gravedad existente en ese lugar.

Tipos de presión y unidades de medida

TIPOS DE PRESIÓN Y UNIDADES DE MEDIDA

La fuerza aplicada sobre un área determinada recibe el nombre de presión. Su expresión matemática es:

            F

P=       A 
Las unidades que se utiliza en el SI son :

P= presión (N/m2)
F= fuerza(N)
A= area (m2)

La presión sobre una superficie aumenta en relación a la fuerza que se le aplica de manera proporcional. Esto quiere decir que si aumentamos al doble la fuerza entonces la fuerza se aumenta al doble.
A mar área la fuerza se distribuye en toda superficie, haciendo que la presión se vea reducida. En cambio, cuando se aplica fuerza a un área pequeña la presión aumenta, debido a que la fuerza se concentra a un solo punto.

Unidades de presión

Unidad		Factor	Unidad de conversión
Atmosfera Corresponde a la presión "tipo" al nivel del mar.		1.03322745	kilos por cm2
		2.27787662	libras por cm2
		14.69594878	libras por pulgada cuadrada
		29.92125984	pulgadas de mercurio
		33.89853848	pies de agua
	*	760	milimetros de mercurio
	*	1013.25	milibares
		1033.22745280	centímetros de agua
	*	1013.250	dinas por cm2
Bar	*	1000	milibares
	*	1000000	barias
	*	1000000	dinas por cm2
Kilo por centímetro cuadrado		0.96784111	atmósferas
		2.20462262	libras por cm2
		14.22334331	libras por pulgada cuadrada
	*	980.665	milibares
	*	1000	centímetros de agua
		980665	dinas por cm2
Libra por centímetro cuadrado		0.43900534	atmósferas
		2.92639653	kilos por pulgada cuadrada
	*	6.4516	libras por pulgada cuadrada
		13.13559287	pulgadas de mercurio
		14.88163944	pies de agua
		333.64405898	milímetros de mercurio
		444.82216153	milibares
	*	453.59237	gramos por cm2
Libra por pulgada cuadrada		0.06804596	atmósferas
		0.15500031	libras por cm2
		2.03602097	pulgadas de mercurio
		2.30665873	pies de agua
		51.71493257	milímetros de mercurio
		68.94757293	milibares
		70.30695796	gramos por cm2
Pulgada de mercurio		0.03342105	atmósferas
		0.07612903	libras por cm2
		0.49115408	libras por pulgada cuadrada
		1.13292484	pies de agua
	*	25.4	milímetros de mercurio
		33.86388158	milibares
		34.53154908	gramos por cm2
Pie de agua		0.02949980	atmósferas
		0.06719690	libras por cm2
		0.43352750	libras por pulgada cuadrada
		0.88267109	pulgadas de mercurio
		22.41984564	milímetros de mercurio
		29.8906692	milibares
		30.48	gramos por cm2
Milímetro de mercurio		0.00131579	atmósferas
		0.00299721	libras por cm2
		0.01933677	libras por pulgada cuadrada
		0.03937008	pulgadas de mercurio
		0.04460334	pies de agua
		1.33322368	milibares
		1.35950981	gramos por cm2
	*	1333.22368421	dinas por cm2
Milibar		0.00098692	atmósferas
	*	0.001	bar
		0.00224809	libras por cm2
		0.01450377	libras por pulgada cuadrada
		0.02952999	pulgadas de mercurio
		0.03345526	pies de agua
		0.75006168	milímetros de mercurio
		1.01971621	gramos por cm2
	*	1000	dinas por cm2
Gramo por centimetro cuadrado		0.00096784	atmósferas
		0.00220462	libras por cm2
		0.01422334	libras por pulgada cuadrada
		0.02895903	pulgadas de mercurio
		0.03280840	pies de agua
		0.73555924	milímetros de mercurio
	*	0.980665	milibares
	*	1	centímetro de agua
	*	980.665	dinas por cm2
Centímetro de agua		0.980665	milibares
	*	1	gramo por cm2
Dina por centímetro cuadrado		0.00000099	atmósferas
	*	0.000001	bar
	*	0.001	milibar
		0.00101972	gramos por cm2
	*	1	baria

las equivalencias mas usuales para conversión de unidades de presión son:

1 lb/ plg2= 6894.76 Pa

1kg/cm2 = 14.22 lb/plg2

1kg/cm2 =98061.6 Pa

presión hidrostatica: se define como la fuerza que ejerce un liquido en reposo sobre la superficie de las paredes del recipiente que lo contiene. Esta fuerza es  perpendicular de las paredes del recipiente. El valor de la presión depende de la naturaleza del liquido y la accion de la gravedad.

La presión para un fluido es la misma a una determinada profundidad a la que se mide. Por ejemplo imagina una columna de liquido contenido en recipiente, a medida que la profundidad aumenta, la masa del agua es mayor con respecto a la parte superior del fluido y, por tanto, su peso es mayor.

Si deseamos calcular la presión hidrostatica debemos considerar la masa del liquido tomando en cuenta su densidad, para ello recordamos la formula de densidad anterior.

                                      P= m

                                           V

Despejado tenemos: m= pV

Y con la formula de peso : W = mg , tenemos lo siguiente: W = pVg , y considerando que el volumen es V= Ah , obtenemos W = pAhg 

Finalmente, como el peso es una fuerza, entonces W = F , despejando el area obtenemos: F= pgh

                                                                                                                                               A

Por lo tanto se obtiene la ecuación matemática: Ph= pgh

PRESIÓN ATMOSFÉRICA:

La presión atmosférica es la presión que ejercen los gases de la atmósfera sobre los cuerpos que se encuentran por debajo de ella, de igual forma con los líquidos. Por ejemplo, la presión arterial depende depende de la presión atmosférica y es un signo vital medido por los médicos para conocer el estado de salud de un individuo.

El hecho de estar rodeados por una masa gaseosa (aire), y al tener este aire un peso actuando sobre la tierra, quiere decir que estamos sometidos a una presión (atmosférica), la presión ejercida por la atmósfera de la tierra, tal como se mide normalmente por medio del barómetro (presión barométrica). Al nivel del mar o a las alturas próximas a este, el valor de la presión es cercano a 14.7 lb/plg² (760 mmHg), disminuyendo estos valores con la altitud.

TABLA DE ALTITUDES Y PRESIONES ATMOSFERICAS 

EQUIVALENCIAS ATMOSFÉRICAS

Por lo general, la presión atmosférica se mide en atmósfera (atm), y una atmósfera es la presión que ejerce que ejerce con una columna de mercurio de 76 cm de altura por cm2 de sección transversal a una temperatura de 0° C.